Рассмотрим ряд продаж вин в Австралии (ежемесячно, в тысячах литров), с января 1980 г. по июнь 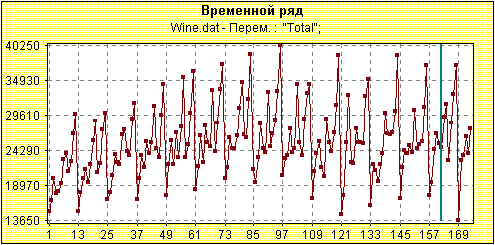1994 (рис.1). Исходные данные - файл wine.dat, переменная "Total".

Рис.1. Продажа вин в Австралии (помесячно, в тысячах литров), с января 1980 г. по июнь 1994 .

Наша цель - построить прогноз на год вперед. Один из критериев правильности прогноза - это его устойчивость. Поэтому сделаем прогноз разными ("гусеничными") способами с помощью нашей программы, в которой реализованы два метода прогноза - аналитический и геометрический.

1. По первым 162 точкам построим аналитический прогноз на 24 точки вперед. Заодно по точкам 163-174 проверим качество прогноза (рис.2).
2. По всему ряду построим прогноз на 12 точек с помощью аналитического метода прогноза (рис.3).
3. По всему ряду построим прогноз на 12 точек с помощью геометрического метода прогноза (рис.4).

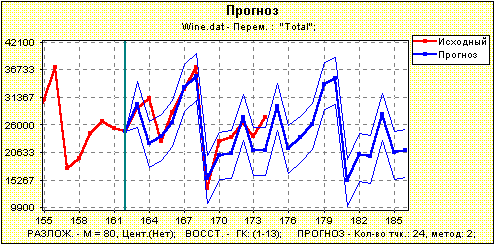
Рис.2. Прогноз (аналитический) по первым 162 точкам на 24 точки вперед. По точкам 163-174 можно проверить качество прогноза.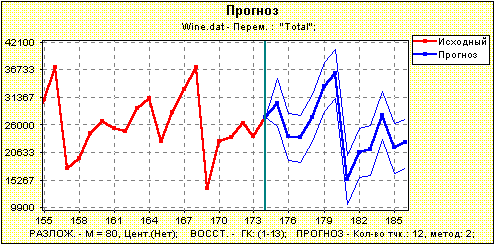

Рис.3. Прогноз (аналитический) по всему ряду на 12 точек вперед.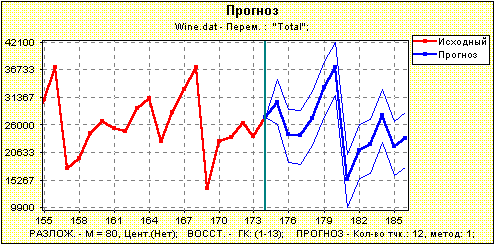

Рис.4. Прогноз (геометрический) по всему ряду на 12 точек вперед.

Теперь проанализируем на примере первого варианта, насколько можно верить доверительным интервалам. Во-первых, отметим, что говорить о доверительных интервалах имеет смысл только в том случае, если прогноз достаточно хороший, так как при построении доверительных интервалов предполагается сохранение и устойчивость структуры ряда, определяемой выбором главных компонент.

Границы доверительных интервалов строятся на основе ошибок прогноза, получаемых при применении формулы прогноза к скользящим участкам ряда. Поэтому следующее предположение состоит в том, что ряд остатков (ошибок), на основе которого строится прогноз, должен состоять из независимых одинаково распределенных случайных величин. В этом случае мы можем пользоваться выборочной моделью. Если, к тому же, остатки нормально распределены, то мы можем применять для построения доверительных границ нормальную модель.

На рис.5 изображены значимости критериев нормальности и независимости для рядов остатков, используемых для построения доверительных границ прогноза на k=1,...,24 шага вперед.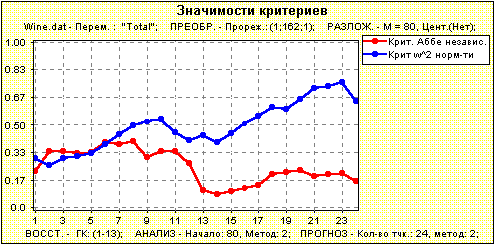

Рис.5. Проверка соответствия модели, по которой строится доверительные интервалы.

Наша программа дает возможность проанализировать более подробно поведение остатков при конкретных значениях k. В частности, на рис.6 изображена автокорреляционная функция остатков для k=1, а на рис.7 проведено сравнение выборочной и нормальной функций распределения (PP-plot).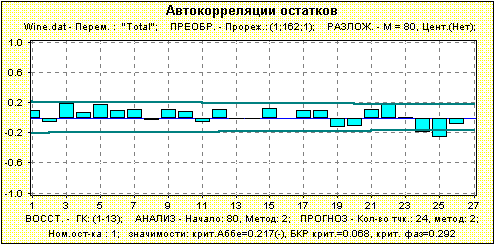

Рис.6. Автокорреляционная функция в целом подтверждает некоррелированность остатков.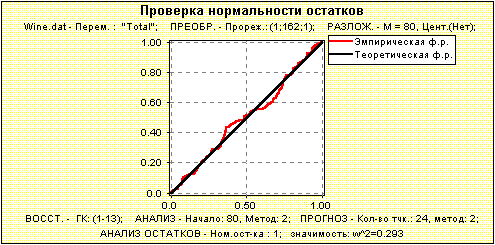

Рис.7. Сравнение функций распределения подтверждает нормальность остатков.

Результаты показывают, что в целом при построении доверительных границ можно пользоваться нормальной моделью. Хотя отметим, что критерий БКР показывает маленькую значимость независимости.

См. также: Прогноз и корни характеристического полинома